Introduction
In the previous article here, we have gone through little-known features about Python int data type. Let’s go through the float data type in this article.
Float data type
Any real value number is represented as float data type such as 0.1, 0.2, 1.234, 56e-4, etc.
The basic arithmetic operations such as addition, subtraction, multiplication, division, floored division, etc. yield the result in float type.

Let’s look into little-known Python float data type features:
Float data type is fixed-precision
The int data type in Python is an arbitrary-precision datatype. It means that you can create an integer object as large as you want but only limited by memory.
On the other hand, the float is a fixed-precision datatype. It means that float objects in Python are represented using a fixed number of bytes. More specifically, the float number is implemented as a double-precision binary float (64-bits) in CPython (standard Python implementation).
How a float data type is stored internally
There are different ways to represent floating-point numbers but IEEE 754 is the most widely used. It consists are 3 parts as shown below:
Sign: As the name suggests it is used to store the sign. 0 indicates positive and 1 indicates a negative number.
Exponent: The exponent field is 11 bits. It can hold values ranging from 0 to 2047 in the case of unsigned integers. For signed numbers, the value ranges from −1022 to +1023. Note that −1023 (all 0s) and +1024 (all 1s) are reserved for special cases.
Mantissa: The next field is mantissa and is 52 bits. It is nothing but all the digits except leading and trailing zeroes. For example, in 000.789, 789000, 78.9000 all three have three significant digits.
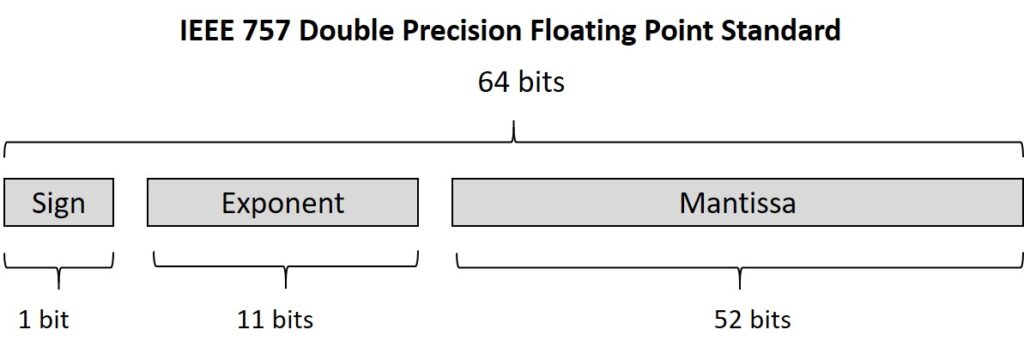
For curious minds, a more detailed description about sign, exponent & mantissa can be found here.
Exact vs. approximate float representation
You know that everything including numbers (int, floats, images, etc.) is stored in binary format in the memory. Float is a fixed-precision data type i.e. it uses a fixed number of bits (64-bits) to represent float numbers. But there are some float numbers that don’t have an exact(finite) binary representation. Let’s try to understand the exact vs. approximate representation of float in binary.
If you need to refresh your memory on how to convert numbers from decimal to binary, check this link.
Exact representation in binary:
It means we can represent float numbers using the exact/finite number of bits in binary.
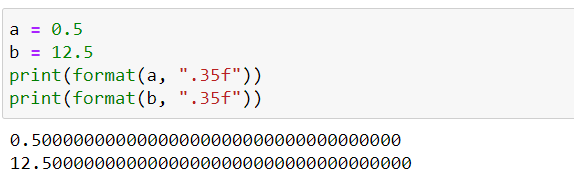
In the above examples, a and b are stored in the binary format using a fixed number of bits. When you read a and b, you will get exact values of 0.5 or 12.5.
Approximate representation in binary:
It means that you won’t be able to represent float numbers using fixed numbers bits in binary. As you can see in the below example, when you convert (0.1)₁₀ to binary, you will get the below value that is in IEEE 754 format. As you just went through it consists of a sign, exponent, and mantissa. In the mantissa part, you notice that 0011 keep repeating over and over again.
Use this link to covert any decimal to IEEE 754 binary float format.
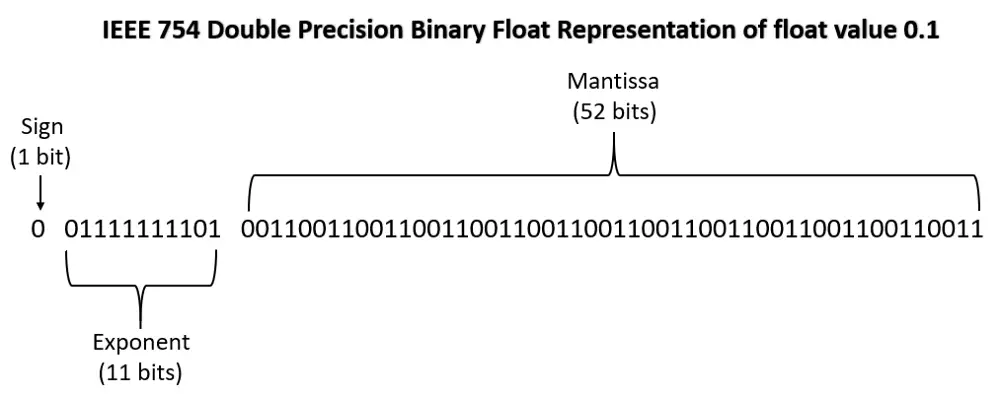
Mantissa can be as large as 52 bits as per the IEEE standard. So, a maximum of 52 bits is considered for the mantissa. This means that you are approximating the mantissa.
So, when you try to display or convert the above binary value to decimal you won’t get exactly (0.1)₁₀ in decimal because you haven’t stored exact representation in binary. Since it was an approximate binary value, you will get the approximate value in decimal as shown below.
Use this link to convert any IEEE 754 binary float to decimal.

You can directly check if a decimal number has an exact or approximate representation using format method as shown below –

d) 0.1 + 0.1 + 0.1 != 0.3
No, I have not lost my mind. Try out yourself. All the floats that don’t have an exact representation in binary will give similar results because they are approximate values. You can look into a few examples below:
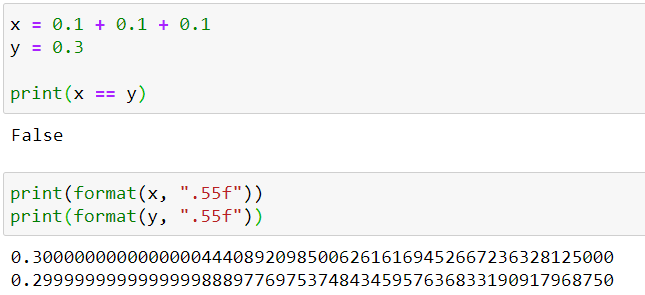
So, as shown in the above example, you will run into issues when you try to compare float values that don’t have an exact binary representation. Let’s look into the solution for this in the next section.
e) How to compare float numbers?
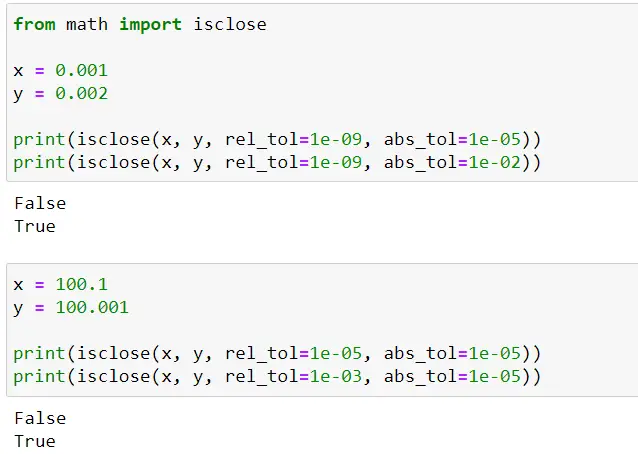
Having understood about finite (exact) vs. infinite (approximate) representation of float numbers, you should be careful when using equality operator (==) with floating numbers as it will return false. The isclose method found in the math module helps to compare float numbers efficiently.
isclose(x, y, *, rel_tol=1e-09, abs_tol=0.0)
x & y: the two float numbers that we want to compare.
rel_tol (relative tolerance): it is the maximum difference for being considered “close”, relative to the magnitude of the input values.
abs_tol (absolute tolerance): it is the maximum difference for being considered “close”, regardless of the magnitude of the input values.
The below two examples will help you understand how to use isclose method for comparing float numbers.
f) float coercion
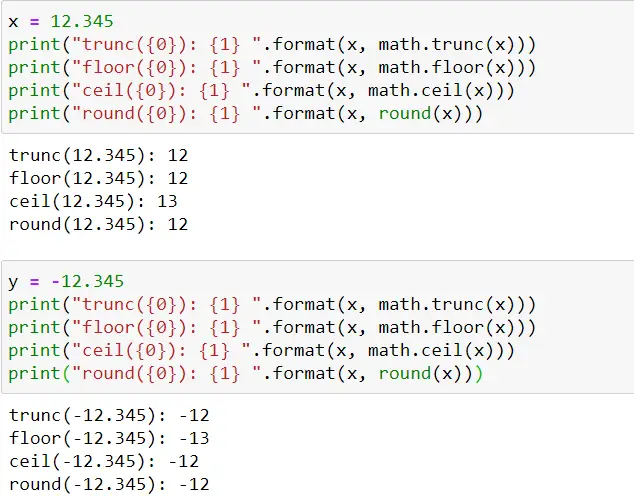
There 4 different ways you can coerce float to integer — truncation, floor, ceiling & rounding.
Truncation — Truncation considers only the value before the decimal point and ignores everything after the decimal point.
Floor — Floor operation returns the largest integer less than or equal to the given number.
Ceiling — Ceiling operation returns the smallest integer greater than or equal to the given number.
Rounding — Rounding returns the closest number that is multiple of 10⁻ⁿ. If ndigits is not passed to round function it returns an integer. Otherwise, it returns the closest number that is multiple of 10⁻ⁿ where n is ndigits.
Except rounding, all other functions are available in the math module. For rounding, you can use Python’s in-built round() function. Let’s look into examples:
The below two examples will help you understand how trunc, floor, ceil and round methods work for comparing float numbers.

Conclusion
In this article, you have understood some interesting details about the Python float data type. If you find this article interesting, do share it with your friends and colleagues.
Originally published at Medium on 12 Jan, 2021.

