Introduction
We are all familiar with the float data type. Do you know there exists another data type called decimal that can be used to represent real-valued (floating-point) numbers? As we saw in the previous article, some of the float numbers don’t have an exact representation in binary. This inexactness causes rounding errors. The decimal data type tries to solve this problem by providing a way to represent floating-point numbers using fixed precision.
I strongly suggest you go through the this article to understand about fixed (finite) vs. approximate (infinite) representation of floating-point numbers and their implications.
Why should you understand decimal?
Why should you understand the decimal data type when we already have the float data type to represent floating-point numbers? Here is one explanation you can find in the official documentation —
“Decimal is based on a floating-point model which was designed with people in mind, and necessarily has a paramount guiding principle — computers must provide an arithmetic that works in the same way as the arithmetic that people learn at school.” — excerpt from the decimal arithmetic specification.
The decimal module plays a vital role mainly in accounting/finance related fields where monetary calculations are involved. As mentioned earlier, the decimal type is used to represent floating-point numbers using fixed precision that doesn’t have exact (or finite) representation in binary. So in situations where monetary calculations are involved, you will be better off if you store them as fixed precision to avoid rounding issues.
Look at the example below — 0.3 has an exact representation in decimal i.e. 0.3 itself but in the float version, it is not exactly 0.3 even though it very close to 0.3. Float type stores approximate values for those that don’t have exact/finite representation in binary.
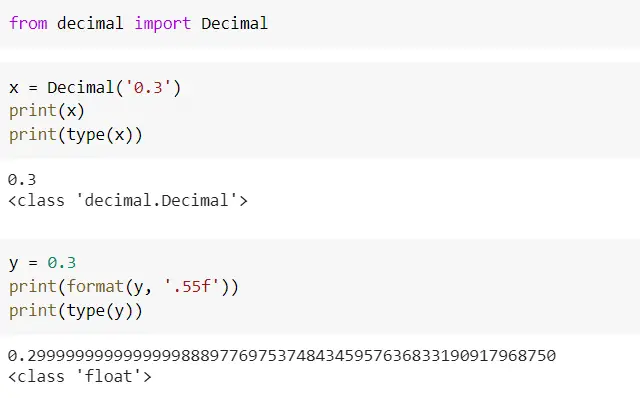
So, how will it impact you?
Refer to the below example. Imagine that you had to sum $12345.01 value 100 million times. The actual result comes to $1234501000000.0 but you are getting the value of $1234501000841.1492. As you can notice there is a difference of $841.149169921875. Even though it may not be a very big number, this will give you nightmares if you are blindly using float and don’t know how it works. Imagine the difference in the amount if the number of floating-point calculations grows even larger. So, in such scenarios, it makes sense to make use of the decimal module instead of the float type.
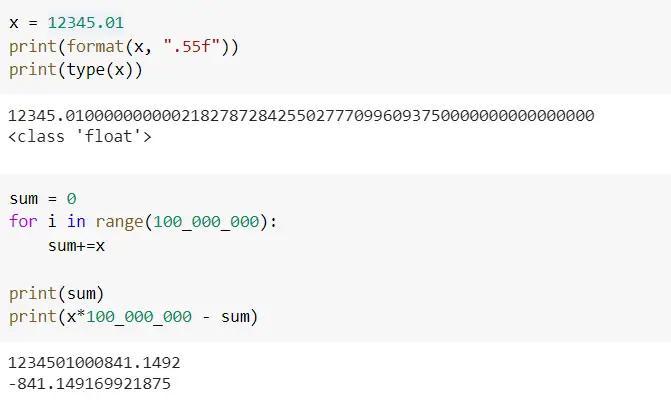
Now that you have understood the importance of the decimal module, let’s focus on how to construct decimals and their usage.
Decimal module
You need to understand three concepts in the decimal module – the decimal number, context for arithmetic, and signals.
a) Decimal number
Like int, float, and string the decimal is also an immutable object. It consists of a sign, coefficients digits, and an exponent. A decimal number also includes +infinity, -infinity, and NaN.
You can construct decimal objects from int, floats, string, tuples, etc. Let’s go through examples of how to construct decimal objects.
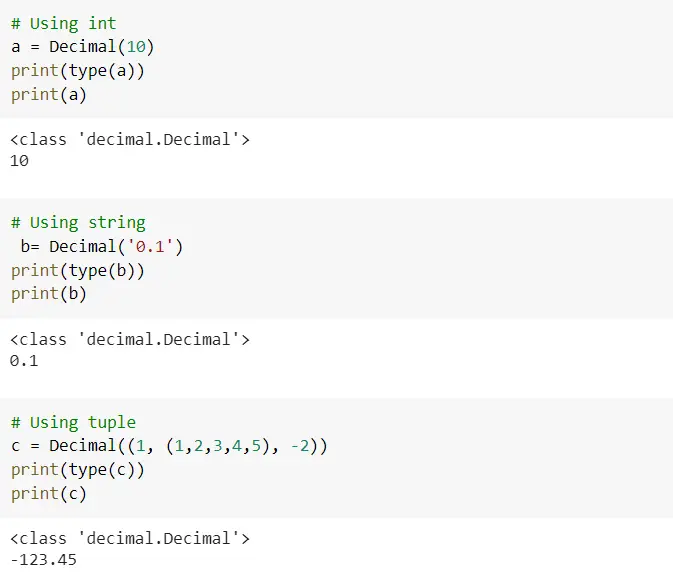
The use of float is not recommended when creating decimals because it will store approximate value instead of fixed precision value. From the below example, as you can see when you try decimal(0.1) it will store the approximate value of 0.1 instead of 0.1 itself.
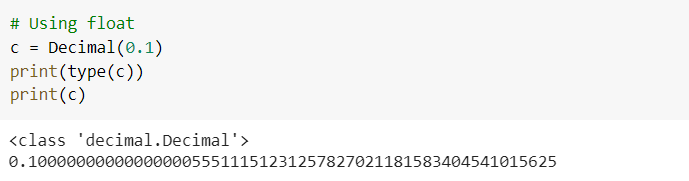
b) Context for arithmetic
The context for arithmetic provides an option to specify/modify the rules for precision, rounding, exponents, enabling traps, flags, etc.
We can get the default context using getcontext() as shown below. It gives default values for precision, rounding, minimum and maximum for the exponent, flags, and traps, etc. Refer to the official documentation PEP 327 for more details on different rounding options and other parameters. For starters, you can mainly look into prec and rounding.
>>> from decimal import getcontext
>>> print(getcontext())
# Output:
# Context(prec=28, rounding=ROUND_HALF_EVEN, Emin=-999999, Emax=999999, capitals=1, clamp=0, flags=[FloatOperation], traps=[InvalidOperation, DivisionByZero, Overflow])
How to use context
When working with real-valued (floating-point) numbers, you can modify (or set the contexts) the default values for precision, rounding, etc. globally as per your need. This way you can work with floating-point numbers efficiently without worrying about rounding errors.
One way to modify the default context is by accessing the attributes of getcontext() using the dot notation and assigning a new value. For example, getcontext().prec = 3 overrides the default precision value from 28 to 3.
The below example shows how we can modify the precision using getcontext().prec . You can also try modifying rounding, Emins, Emax, etc.
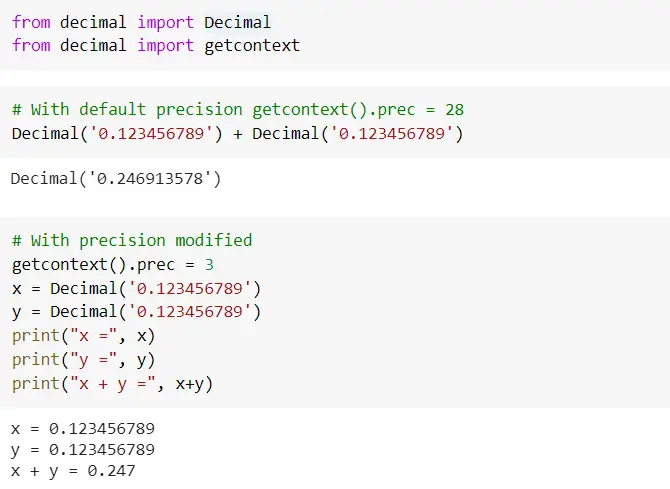
Precision and rounding play their role only during arithmetic operations as is evident from the above example. Even though precision was set to 3, x and y have 9 precisions but only after the arithmetic operation, precision gets reduced to 3.
For the advanced usage of context and its parameters, you can refer to this.
c) Signals
The signals are the exceptional conditions that arise during the decimal mathematical operations. The signals listed in the decimal module are -Clamped, InvalidOperation, DivisionByZero, Inexact, Rounded, Subnormal, Overflow, Underflow, and FloatOperation.
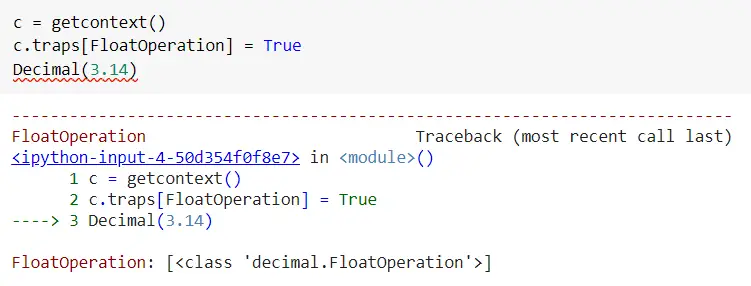
For example, if you don’t want to use float operations in your application with the decimal module then you could trap float operation as below. So, when you try to construct decimal using float it will raise an exception.
Mathematical operations
Decimal supports the basic arithmetic operations — addition (+), subtraction (-), multiplication (*), division (/), div mod (//), module (%).
There is one crucial difference you need to make a note of here. Div mod (//) returns a floored quotient floor(a/b) in the case of integer operations but it returns the truncated quotient trunc(a/b) in the case of decimal types. The floor division and modulo operators are defined in such a way that they always satisfy the below condition for any given two numbers a & b.

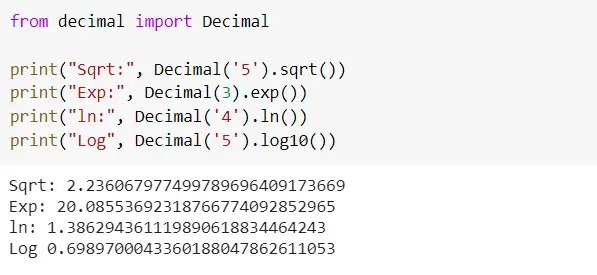
The decimal also supports sqrt, min, max, power, etc. Refer to the below example. You get the result of up to 28 precisions as it the default value as defined in getcontext(). For the mathematical operations that are not included in decimal, you can explore math module.
Float Vs. Decimal
a) Decimal type efficiently handles precision and rounding better than float data type.
b) Since precision and rounding are handled efficiently, the decimal type is highly recommended for situations where monetary calculations are involved.
c) Decimal type consumes a lot more memory than float. On the other hand, float takes less memory. As you can see there is an additional 80 bytes overhead for using decimal type.

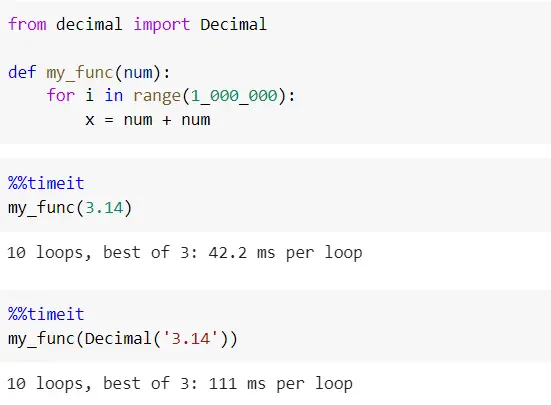
d) The performance of float is better than decimal. If your application is smaller and there are not many operations involved you probably won’t notice the difference in performance but you will start to see the difference when your application grows larger, and the number of decimal operations increases. As seen in the below sample code, float operations are faster than the decimals.
Conclusion
In this article, you have understood decimal data type as an alternative to float type for representing floating-point (real-valued) numbers. Float and Decimal types have their own pros and cons. Though the use of float or decimal depends on the use-case you must also take into consideration its pros and cons when choosing float or decimal.

